RIXS $L_{2,3}M_{1}$
Instead of looking at low energy excitations one can use RIXS to look at core-core excitations. A powerful technique comparable to other core level spectroscopies like x-ray absorption and core-level photoemission at once.
Here a script to calculate the Ni $2p$ to $3d$ excitation ($L_{2,3}$) and Ni $3s$ to $2p$ decay ($M_{1}$).
- RIXS_L23M1.Quanty
-- This example calculates core - core RIXS spectra. These type of spectra are -- highly informative and contain similar information as core level absorption and -- core level photoemission combined. With generally enhances sensitivity. -- we focus here on 2p to 3d excitations (L23) and 3s to 2p decay (final hole in the 3s -- state, the M1 edge) -- We use the definitions of all operators and basis orbitals as defined in the file -- include and can afterwards directly continue by creating the Hamiltonian -- and calculating the spectra dofile("Include.Quanty") -- The parameters and scheme needed is the same as the one used for XAS -- We follow the energy definitions as introduced in the group of G.A. Sawatzky (Groningen) -- J. Zaanen, G.A. Sawatzky, and J.W. Allen PRL 55, 418 (1985) -- for parameters of specific materials see -- A.E. Bockquet et al. PRB 55, 1161 (1996) -- After some initial discussion the energies U and Delta refer to the center of a configuration -- The L^10 d^n configuration has an energy 0 -- The L^9 d^n+1 configuration has an energy Delta -- The L^8 d^n+2 configuration has an energy 2*Delta+Udd -- -- If we relate this to the onsite energy of the L and d orbitals we find -- 10 eL + n ed + n(n-1) U/2 == 0 -- 9 eL + (n+1) ed + (n+1)n U/2 == Delta -- 8 eL + (n+2) ed + (n+1)(n+2) U/2 == 2*Delta+U -- 3 equations with 2 unknowns, but with interdependence yield: -- ed = (10*Delta-nd*(19+nd)*U/2)/(10+nd) -- eL = nd*((1+nd)*Udd/2-Delta)/(10+nd) -- -- For the final state we/they defined -- The 2p^5 L^10 d^n+1 configuration has an energy 0 -- The 2p^5 L^9 d^n+2 configuration has an energy Delta + Udd - Upd -- The 2p^5 L^8 d^n+3 configuration has an energy 2*Delta + 3*Udd - 2*Upd -- -- If we relate this to the onsite energy of the p and d orbitals we find -- 6 ep + 10 eL + n ed + n(n-1) Udd/2 + 6 n Upd == 0 -- 6 ep + 9 eL + (n+1) ed + (n+1)n Udd/2 + 6 (n+1) Upd == Delta -- 6 ep + 8 eL + (n+2) ed + (n+1)(n+2) Udd/2 + 6 (n+2) Upd == 2*Delta+Udd -- 5 ep + 10 eL + (n+1) ed + (n+1)(n) Udd/2 + 5 (n+1) Upd == 0 -- 5 ep + 9 eL + (n+2) ed + (n+2)(n+1) Udd/2 + 5 (n+2) Upd == Delta+Udd-Upd -- 5 ep + 8 eL + (n+3) ed + (n+3)(n+2) Udd/2 + 5 (n+3) Upd == 2*Delta+3*Udd-2*Upd -- 6 equations with 3 unknowns, but with interdependence yield: -- epfinal = (10*Delta + (1+nd)*(nd*Udd/2-(10+nd)*Upd) / (16+nd) -- edfinal = (10*Delta - nd*(31+nd)*Udd/2-90*Upd) / (16+nd) -- eLfinal = ((1+nd)*(nd*Udd/2+6*Upd)-(6+nd)*Delta) / (16+nd) -- -- note that ed-ep = Delta - nd * U and not Delta -- note furthermore that ep and ed here are defined for the onsite energy if the system had -- locally nd electrons in the d-shell. In DFT or Hartree Fock the d occupation is in the end not -- nd and thus the onsite energy of the Kohn-Sham orbitals is not equal to ep and ed in model -- calculations. -- -- note furthermore that ep and eL actually should be different for most systems. We happily ignore this fact -- -- We normally take U and Delta as experimentally determined parameters -- -- besides the two configurations with either no core hole or the configuration with one -- core hole in the 2p shell we now also need a configuration with one core hole in the -- 3s shell -- -- We define: -- The 3s^1 L^10 d^n+1 configuration has an energy 0 -- The 3s^1 L^9 d^n+2 configuration has an energy Delta + Udd - Usd -- The 3s^1 L^8 d^n+3 configuration has an energy 2*Delta + 3*Udd - 2*Usd -- -- If we relate this to the onsite energy of the s and d orbitals we find -- 2 es + 10 eL + n ed + n(n-1) Udd/2 + 2 n Usd == 0 -- 2 es + 9 eL + (n+1) ed + (n+1)n Udd/2 + 2 (n+1) Usd == Delta -- 2 es + 8 eL + (n+2) ed + (n+1)(n+2) Udd/2 + 2 (n+2) Usd == 2*Delta+Udd -- 1 es + 10 eL + (n+1) ed + (n+1)(n) Udd/2 + 1 (n+1) Usd == 0 -- 1 es + 9 eL + (n+2) ed + (n+2)(n+1) Udd/2 + 1 (n+2) Usd == Delta+Udd-Usd -- 1 es + 8 eL + (n+3) ed + (n+3)(n+2) Udd/2 + 1 (n+3) Usd == 2*Delta+3*Udd-2*Usd -- -- 6 equations with 3 unknowns, but with interdependence yield: -- eswiths = (10*Delta + (1+nd)*(nd*Udd/2-(10+nd)*Usd) / (12+nd) -- edwiths = (10*Delta - nd*(23+nd)*Udd/2-22*Usd) / (12+nd) -- eLwiths = ((1+nd)*(nd*Udd/2+2*Usd)-(2+nd)*Delta) / (12+nd) -- number of electrons (formal valence) nd = 8 -- parameters from experiment (core level PES) Udd = 7.3 Upd = 8.5 Usd = 6.0 Delta = 4.7 -- parameters obtained from DFT (PRB 85, 165113 (2012)) F2dd = 11.14 F4dd = 6.87 F2pd = 6.67 G1pd = 4.92 G3pd = 2.80 G2sd = 12.56 tenDq = 0.56 tenDqL = 1.44 Veg = 2.06 Vt2g = 1.21 zeta_3d = 0.081 zeta_2p = 11.51 Bz = 0.000001 H112 = 0.120 ed = (10*Delta-nd*(19+nd)*Udd/2)/(10+nd) eL = nd*((1+nd)*Udd/2-Delta)/(10+nd) epfinal = (10*Delta + (1+nd)*(nd*Udd/2-(10+nd)*Upd)) / (16+nd) edfinal = (10*Delta - nd*(31+nd)*Udd/2-90*Upd) / (16+nd) eLfinal = ((1+nd)*(nd*Udd/2+6*Upd) - (6+nd)*Delta) / (16+nd) eswiths = (10*Delta + (1+nd)*(nd*Udd/2-(10+nd)*Usd)) / (12+nd) edwiths = (10*Delta - nd*(23+nd)*Udd/2-22*Usd) / (12+nd) eLwiths = ((1+nd)*(nd*Udd/2+2*Usd) - (2+nd)*Delta) / (12+nd) F0dd = Udd + (F2dd+F4dd) * 2/63 F0pd = Upd + (1/15)*G1pd + (3/70)*G3pd F0sd = Usd + G2sd/10 Hamiltonian = F0dd*OppF0_3d + F2dd*OppF2_3d + F4dd*OppF4_3d + zeta_3d*Oppldots_3d + Bz*(2*OppSz_3d + OppLz_3d) + H112 * (OppSx_3d+OppSy_3d+2*OppSz_3d)/sqrt(6) + tenDq*OpptenDq_3d + tenDqL*OpptenDq_Ld + Veg * OppVeg + Vt2g * OppVt2g + ed * OppN_3d + eL * OppN_Ld XASHamiltonian = F0dd*OppF0_3d + F2dd*OppF2_3d + F4dd*OppF4_3d + zeta_3d*Oppldots_3d + Bz*(2*OppSz_3d + OppLz_3d) + H112 * (OppSx_3d+OppSy_3d+2*OppSz_3d)/sqrt(6) + tenDq*OpptenDq_3d + tenDqL*OpptenDq_Ld + Veg * OppVeg + Vt2g * OppVt2g + edfinal * OppN_3d + eLfinal * OppN_Ld + epfinal * OppN_2p + zeta_2p * Oppcldots + F0pd * OppUpdF0 + F2pd * OppUpdF2 + G1pd * OppUpdG1 + G3pd * OppUpdG3 Hamiltonian3s = F0dd*OppF0_3d + F2dd*OppF2_3d + F4dd*OppF4_3d + zeta_3d*Oppldots_3d + Bz*(2*OppSz_3d + OppLz_3d) + H112 * (OppSx_3d+OppSy_3d+2*OppSz_3d)/sqrt(6) + tenDq*OpptenDq_3d + tenDqL*OpptenDq_Ld + Veg * OppVeg + Vt2g * OppVt2g + edwiths * OppN_3d + eLwiths * OppN_Ld + eswiths * OppN_3s + F0sd * OppUsdF0 + G2sd * OppUsdG2 -- we now can create the lowest Npsi eigenstates: Npsi=3 -- in order to make sure we have a filling of 8 electrons we need to define some restrictions StartRestrictions = {NF, NB, {"000000 00 1111111111 0000000000",8,8}, {"111111 11 0000000000 1111111111",18,18}} psiList = Eigensystem(Hamiltonian, StartRestrictions, Npsi) oppList={Hamiltonian, OppSsqr, OppLsqr, OppJsqr, OppSx_3d, OppLx_3d, OppSy_3d, OppLy_3d, OppSz_3d, OppLz_3d, Oppldots_3d, OppF2_3d, OppF4_3d, OppNeg_3d, OppNt2g_3d, OppNeg_Ld, OppNt2g_Ld, OppN_3d} -- print of some expectation values print(" # <E> <S^2> <L^2> <J^2> <S_x^3d> <L_x^3d> <S_y^3d> <L_y^3d> <S_z^3d> <L_z^3d> <l.s> <F[2]> <F[4]> <Neg^3d> <Nt2g^3d><Neg^Ld> <Nt2g^Ld><N^3d>"); for i = 1,#psiList do io.write(string.format("%3i ",i)) for j = 1,#oppList do expectationvalue = Chop(psiList[i]*oppList[j]*psiList[i]) io.write(string.format("%8.3f ",expectationvalue)) end io.write("\n") end -- spectra XAS XASSpectra = CreateSpectra(XASHamiltonian, T2p3dx, psiList[1], {{"Emin",-10}, {"Emax",20}, {"NE",3500}, {"Gamma",1.0}}) XASSpectra.Print({{"file","RIXSL23M1_XAS.dat"}}) -- spectra FY FYSpectra = CreateFluorescenceYield(XASHamiltonian, T2p3dx, T3s2py, psiList[1], {{"Emin",-10}, {"Emax",20}, {"NE",3500}, {"Gamma",1.0}}) FYSpectra.Print({{"file","RIXSL23M1_FY.dat"}}) -- spectra RIXS RIXSSpectra = CreateResonantSpectra(XASHamiltonian, Hamiltonian3s, T2p3dx, T3s2py, psiList[1], {{"Emin1",-10}, {"Emax1",20}, {"NE1",120}, {"Gamma1",1.0}, {"Emin2",-1}, {"Emax2",9}, {"NE2",1000}, {"Gamma2",0.5}}) RIXSSpectra.Print({{"file","RIXSL23M1.dat"}}) print("Finished calculating the spectra now start plotting.\nThis might take more time than the calculation"); -- and make some plots gnuplotInput = [[ set autoscale set xtic auto set ytic auto set style line 1 lt 1 lw 1 lc rgb "#000000" set style line 2 lt 1 lw 1 lc rgb "#FF0000" set style line 3 lt 1 lw 1 lc rgb "#00FF00" set style line 4 lt 1 lw 1 lc rgb "#0000FF" set out 'RIXSL23M1_Map.ps' set terminal postscript portrait enhanced color "Times" 8 size 7.5,6 unset colorbox energyshift=857.6 energyshiftM1=110.8 set multiplot set size 0.5,0.55 set origin 0,0 set ylabel "resonant energy (eV)" font "Times,10" set xlabel "energy loss (eV)" font "Times,10" set yrange [852:860] set xrange [energyshiftM1-0.5:energyshiftM1+7.5] plot "<(awk '((NR>5)&&(NR<1007)){for(i=3;i<=NF;i=i+2){printf \"%s \", $i}{printf \"%s\", RS}}' RIXSL23M1.dat)" matrix using ($2/100-1.0+energyshiftM1):($1/4+energyshift-10):(-$3) with image notitle set origin 0.5,0 set yrange [869:877] set xrange [energyshiftM1-0.5:energyshiftM1+7.5] plot "<(awk '((NR>5)&&(NR<1007)){for(i=3;i<=NF;i=i+2){printf \"%s \", $i}{printf \"%s\", RS}}' RIXSL23M1.dat)" matrix using ($2/100-1.0+energyshiftM1):($1/4+energyshift-10):(-$3) with image notitle unset multiplot set out 'RIXSL23M1_Spec.ps' set size 1.0, 1.0 set terminal postscript portrait enhanced color "Times" 8 size 7.5,5 set multiplot set size 0.25,1.0 set origin 0,0 set ylabel "E (eV)" font "Times,10" set xlabel "XAS" font "Times,10" set yrange [energyshift-10:energyshift+20] set xrange [-0.3:0] plot "RIXSL23M1_XAS.dat" using 3:($1+energyshift) notitle with lines ls 1,\ "RIXSL23M1_FY.dat" using (-5*$2):($1+energyshift) notitle with lines ls 4 set size 0.8,1.0 set origin 0.2,0.0 set xlabel "Energy loss (eV)" font "Times,10" unset ylabel unset ytics set xrange [energyshiftM1-0.5:energyshiftM1+7.5] ofset = 0.25 scale=10 plot for [i=0:120] "RIXSL23M1.dat" using ($1+energyshiftM1):(-column(3+2*i)*scale+ofset*i-10 + energyshift) notitle with lines ls 4 unset multiplot ]] -- write the gnuplot script to a file file = io.open("RIXSL23M1.gnuplot", "w") file:write(gnuplotInput) file:close() -- call gnuplot to execute the script os.execute("gnuplot RIXSL23M1.gnuplot") -- transform to pdf and eps os.execute("ps2pdf RIXSL23M1_Map.ps ; ps2eps RIXSL23M1_Map.ps ; mv RIXSL23M1_Map.eps temp.eps ; eps2eps temp.eps RIXSL23M1_Map.eps ; rm temp.eps") os.execute("ps2pdf RIXSL23M1_Spec.ps ; ps2eps RIXSL23M1_Spec.ps ; mv RIXSL23M1_Spec.eps temp.eps ; eps2eps temp.eps RIXSL23M1_Spec.eps ; rm temp.eps")
Just like in the case of $L_{2,3}M_{4,5}$ edge RIXS we can make plots:
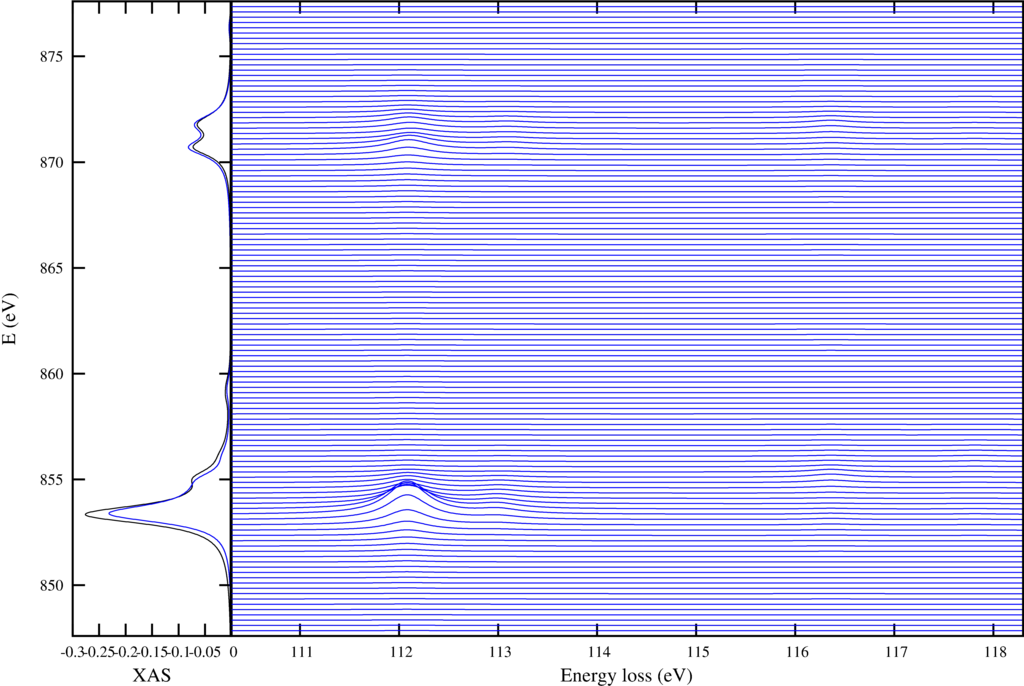 |
| Resonant inelastic x-ray scattering spectra for different incoming and outgoing photon energies. |
|---|
The first shows on the left the XAS spectra in black and the integrated RIXS spectra (FY) in blue. The core-core RIXS is shown on the right.
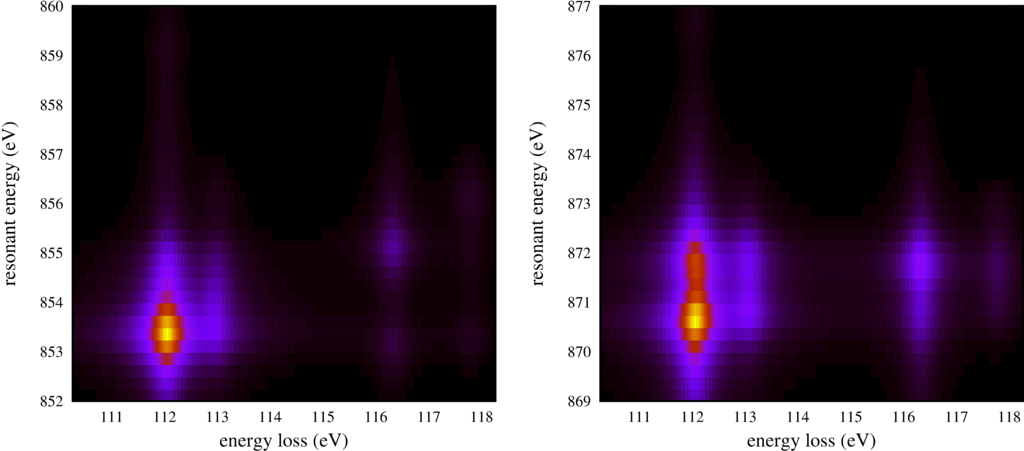 |
| Resonant inelastic x-ray scattering spectra for different incoming and outgoing photon energies. |
|---|
The second plot shows the same RIXS spectra, but now as an intensity map.
The output of the script is:
- RIXS_L23M1.out
# <E> <S^2> <L^2> <J^2> <S_x^3d> <L_x^3d> <S_y^3d> <L_y^3d> <S_z^3d> <L_z^3d> <l.s> <F[2]> <F[4]> <Neg^3d> <Nt2g^3d><Neg^Ld> <Nt2g^Ld><N^3d> 1 -3.503 1.999 12.000 15.095 -0.370 -0.115 -0.370 -0.115 -0.741 -0.230 -0.305 -1.042 -0.924 2.186 5.990 3.825 6.000 8.175 2 -3.395 1.999 12.000 15.160 -0.002 -0.000 -0.002 -0.000 -0.003 -0.001 -0.322 -1.043 -0.925 2.189 5.988 3.823 6.000 8.178 3 -3.286 1.999 12.000 15.211 0.369 0.113 0.369 0.113 0.737 0.227 -0.336 -1.043 -0.925 2.193 5.987 3.820 6.000 8.180 Start of LanczosTriDiagonalizeKrylovMC Start of LanczosTriDiagonalizeKrylovMC Finished calculating the spectra now start plotting. This might take more time than the calculation