Energy level diagram
In order to do temperature averaging it is important to understand the number of excited states that are important. One can learn a lot by looking at the energy level diagram. Here we plot one for Ni$^{2+}$.
The input file is:
- Energy_level_diagram.Quanty
Verbosity(0) -- In order to understand the physics / chemistry of a system it is often good -- to make energy level diagrams. i.e. plot the eigen-state energy as a function -- of some parameter one varies. -- Here we create the energy level diagram of all 190 states of NiO in the ligand -- field approximation as a function of the Ni onsite crystal-field strenght NF=20 NB=0 IndexDn_3d={ 0, 2, 4, 6, 8} IndexUp_3d={ 1, 3, 5, 7, 9} IndexDn_Ld={10,12,14,16,18} IndexUp_Ld={11,13,15,17,19} -- angular momentum operators on the d-shell OppSx_3d =NewOperator("Sx" ,NF, IndexUp_3d, IndexDn_3d) OppSy_3d =NewOperator("Sy" ,NF, IndexUp_3d, IndexDn_3d) OppSz_3d =NewOperator("Sz" ,NF, IndexUp_3d, IndexDn_3d) OppSsqr_3d =NewOperator("Ssqr" ,NF, IndexUp_3d, IndexDn_3d) OppSplus_3d=NewOperator("Splus",NF, IndexUp_3d, IndexDn_3d) OppSmin_3d =NewOperator("Smin" ,NF, IndexUp_3d, IndexDn_3d) OppLx_3d =NewOperator("Lx" ,NF, IndexUp_3d, IndexDn_3d) OppLy_3d =NewOperator("Ly" ,NF, IndexUp_3d, IndexDn_3d) OppLz_3d =NewOperator("Lz" ,NF, IndexUp_3d, IndexDn_3d) OppLsqr_3d =NewOperator("Lsqr" ,NF, IndexUp_3d, IndexDn_3d) OppLplus_3d=NewOperator("Lplus",NF, IndexUp_3d, IndexDn_3d) OppLmin_3d =NewOperator("Lmin" ,NF, IndexUp_3d, IndexDn_3d) OppJx_3d =NewOperator("Jx" ,NF, IndexUp_3d, IndexDn_3d) OppJy_3d =NewOperator("Jy" ,NF, IndexUp_3d, IndexDn_3d) OppJz_3d =NewOperator("Jz" ,NF, IndexUp_3d, IndexDn_3d) OppJsqr_3d =NewOperator("Jsqr" ,NF, IndexUp_3d, IndexDn_3d) OppJplus_3d=NewOperator("Jplus",NF, IndexUp_3d, IndexDn_3d) OppJmin_3d =NewOperator("Jmin" ,NF, IndexUp_3d, IndexDn_3d) Oppldots_3d=NewOperator("ldots",NF, IndexUp_3d, IndexDn_3d) -- Angular momentum operators on the Ligand shell OppSx_Ld =NewOperator("Sx" ,NF, IndexUp_Ld, IndexDn_Ld) OppSy_Ld =NewOperator("Sy" ,NF, IndexUp_Ld, IndexDn_Ld) OppSz_Ld =NewOperator("Sz" ,NF, IndexUp_Ld, IndexDn_Ld) OppSsqr_Ld =NewOperator("Ssqr" ,NF, IndexUp_Ld, IndexDn_Ld) OppSplus_Ld=NewOperator("Splus",NF, IndexUp_Ld, IndexDn_Ld) OppSmin_Ld =NewOperator("Smin" ,NF, IndexUp_Ld, IndexDn_Ld) OppLx_Ld =NewOperator("Lx" ,NF, IndexUp_Ld, IndexDn_Ld) OppLy_Ld =NewOperator("Ly" ,NF, IndexUp_Ld, IndexDn_Ld) OppLz_Ld =NewOperator("Lz" ,NF, IndexUp_Ld, IndexDn_Ld) OppLsqr_Ld =NewOperator("Lsqr" ,NF, IndexUp_Ld, IndexDn_Ld) OppLplus_Ld=NewOperator("Lplus",NF, IndexUp_Ld, IndexDn_Ld) OppLmin_Ld =NewOperator("Lmin" ,NF, IndexUp_Ld, IndexDn_Ld) OppJx_Ld =NewOperator("Jx" ,NF, IndexUp_Ld, IndexDn_Ld) OppJy_Ld =NewOperator("Jy" ,NF, IndexUp_Ld, IndexDn_Ld) OppJz_Ld =NewOperator("Jz" ,NF, IndexUp_Ld, IndexDn_Ld) OppJsqr_Ld =NewOperator("Jsqr" ,NF, IndexUp_Ld, IndexDn_Ld) OppJplus_Ld=NewOperator("Jplus",NF, IndexUp_Ld, IndexDn_Ld) OppJmin_Ld =NewOperator("Jmin" ,NF, IndexUp_Ld, IndexDn_Ld) -- total angular momentum OppSx = OppSx_3d + OppSx_Ld OppSy = OppSy_3d + OppSy_Ld OppSz = OppSz_3d + OppSz_Ld OppSsqr = OppSx * OppSx + OppSy * OppSy + OppSz * OppSz OppLx = OppLx_3d + OppLx_Ld OppLy = OppLy_3d + OppLy_Ld OppLz = OppLz_3d + OppLz_Ld OppLsqr = OppLx * OppLx + OppLy * OppLy + OppLz * OppLz OppJx = OppJx_3d + OppJx_Ld OppJy = OppJy_3d + OppJy_Ld OppJz = OppJz_3d + OppJz_Ld OppJsqr = OppJx * OppJx + OppJy * OppJy + OppJz * OppJz -- define the coulomb operator -- we here define the part depending on F0 seperately from the part depending on F2 -- when summing we can put in the numerical values of the slater integrals OppF0_3d =NewOperator("U", NF, IndexUp_3d, IndexDn_3d, {1,0,0}) OppF2_3d =NewOperator("U", NF, IndexUp_3d, IndexDn_3d, {0,1,0}) OppF4_3d =NewOperator("U", NF, IndexUp_3d, IndexDn_3d, {0,0,1}) -- define onsite energies - crystal field -- Akm = {{k1,m1,Akm1},{k2,m2,Akm2}, ... } Akm = PotentialExpandedOnClm("Oh", 2, {0.6,-0.4}) OpptenDq_3d = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, Akm) OpptenDq_Ld = NewOperator("CF", NF, IndexUp_Ld, IndexDn_Ld, Akm) Akm = PotentialExpandedOnClm("Oh", 2, {1,0}) OppNeg_3d = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, Akm) OppNeg_Ld = NewOperator("CF", NF, IndexUp_Ld, IndexDn_Ld, Akm) Akm = PotentialExpandedOnClm("Oh", 2, {0,1}) OppNt2g_3d = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, Akm) OppNt2g_Ld = NewOperator("CF", NF, IndexUp_Ld, IndexDn_Ld, Akm) OppNUp_3d = NewOperator("Number", NF, IndexUp_3d, IndexUp_3d, {1,1,1,1,1}) OppNDn_3d = NewOperator("Number", NF, IndexDn_3d, IndexDn_3d, {1,1,1,1,1}) OppN_3d = OppNUp_3d + OppNDn_3d OppNUp_Ld = NewOperator("Number", NF, IndexUp_Ld, IndexUp_Ld, {1,1,1,1,1}) OppNDn_Ld = NewOperator("Number", NF, IndexDn_Ld, IndexDn_Ld, {1,1,1,1,1}) OppN_Ld = OppNUp_Ld + OppNDn_Ld -- define L-d interaction Akm = PotentialExpandedOnClm("Oh",2,{1,0}) OppVeg = NewOperator("CF", NF, IndexUp_3d,IndexDn_3d, IndexUp_Ld,IndexDn_Ld,Akm) + NewOperator("CF", NF, IndexUp_Ld,IndexDn_Ld, IndexUp_3d,IndexDn_3d,Akm) Akm = PotentialExpandedOnClm("Oh",2,{0,1}) OppVt2g = NewOperator("CF", NF, IndexUp_3d,IndexDn_3d, IndexUp_Ld,IndexDn_Ld,Akm) + NewOperator("CF", NF, IndexUp_Ld,IndexDn_Ld, IndexUp_3d,IndexDn_3d,Akm) -- We follow the energy definitions as introduced in the group of G.A. Sawatzky (Groningen) -- J. Zaanen, G.A. Sawatzky, and J.W. Allen PRL 55, 418 (1985) -- for parameters of specific materials see -- A.E. Bockquet et al. PRB 55, 1161 (1996) -- After some initial discussion the energies U and Delta refer to the center of a configuration -- The L^10 d^n configuration has an energy 0 -- The L^9 d^n+1 configuration has an energy Delta -- The L^8 d^n+2 configuration has an energy 2*Delta+U -- -- If we relate this to the onsite energy of the p and d orbitals we find -- 10 eL + n ed + n(n-1) U/2 == 0 -- 9 eL + (n+1) ed + (n+1)n U/2 == Delta -- 8 eL + (n+2) ed + (n+1)(n+2) U/2 == 2*Delta+U -- 3 equations with 2 unknowns, but with interdependence yield: -- ed = (10*Delta-nd*(19+nd)*U/2)/(10+nd) -- ep = nd*((1+nd)*U/2-Delta)/(10+nd) -- -- note that ed-ep = Delta - nd * U and not Delta -- note furthermore that ep and ed here are defined for the onsite energy if the system had -- locally nd electrons in the d-shell. In DFT or Hartree Fock the d occupation is in the end not -- nd and thus the onsite energy of the Kohn-Sham orbitals is not equal to ep and ed in model -- calculations. -- -- note furthermore that ep and eL actually should be different for most systems. We happily ignore this fact -- -- We normally take U and Delta as experimentally determined parameters -- number of electrons (formal valence) nd = 8 -- parameters from experiment (core level PES) U = 7.3 Delta = 4.7 -- parameters obtained from DFT (PRB 85, 165113 (2012)) F2dd = 11.142 F4dd = 6.874 tenDq = 0.56 tenDqL = 1.44 Veg = 2.06 Vt2g = 1.21 zeta_3d = 0.081 Bz = 0.000001 ed = (10*Delta-nd*(19+nd)*U/2)/(10+nd) eL = nd*((1+nd)*U/2-Delta)/(10+nd) F0dd = U+(F2dd+F4dd)*2/63 Hamiltonian0 = F0dd*OppF0_3d + F2dd*OppF2_3d + F4dd*OppF4_3d + zeta_3d*Oppldots_3d + Bz*(2*OppSz_3d + OppLz_3d) + tenDqL*OpptenDq_Ld + Veg * OppVeg + Vt2g * OppVt2g + ed * OppN_3d + eL * OppN_Ld Npsi=190 StartRestrictions = {NF, NB, {"1111111111 0000000000",8,8}, {"0000000000 1111111111",10,10}} psiList = Eigensystem(Hamiltonian0, StartRestrictions, Npsi) file = assert( io.open("EnergyLevelDiagram", "w")) for i=0, 30 do tenDq = 0.1*i file:write(string.format("%14.7E ",tenDq)) Hamiltonian=Hamiltonian0 + tenDq * OpptenDq_3d Eigensystem(Hamiltonian, psiList) for key,value in pairs(psiList) do energy = value * Hamiltonian * value file:write(string.format("%14.7E ",energy)) end file:write("\n") end file:close() gnuplotInput = [[ set autoscale set xtic auto set ytic auto set style line 1 lt 1 lw 1 lc rgb "#000000" set xlabel "10Dq (eV)" font "Times,12" set ylabel "Energy (eV)" font "Times,12" set out 'EnergyLevelDiagram.ps' set size 1.0, 1.0 set terminal postscript portrait enhanced color "Times" 8 plot for [i=2:191] "EnergyLevelDiagram" using 1:i notitle with lines ls 1 ]] -- write the gnuplot script to a file file = io.open("EnergyLevelDiagram.gnuplot", "w") file:write(gnuplotInput) file:close() -- call gnuplot to execute the script os.execute("gnuplot EnergyLevelDiagram.gnuplot") -- change the postscript file to pdf or eps os.execute("ps2pdf EnergyLevelDiagram.ps ; ps2eps EnergyLevelDiagram.ps ; mv EnergyLevelDiagram.eps temp.eps ; eps2eps temp.eps EnergyLevelDiagram.eps ; rm temp.eps")
As in example 4 Quanty returns a nice plot. Note that one can add labeling. For this have a look at example 4.
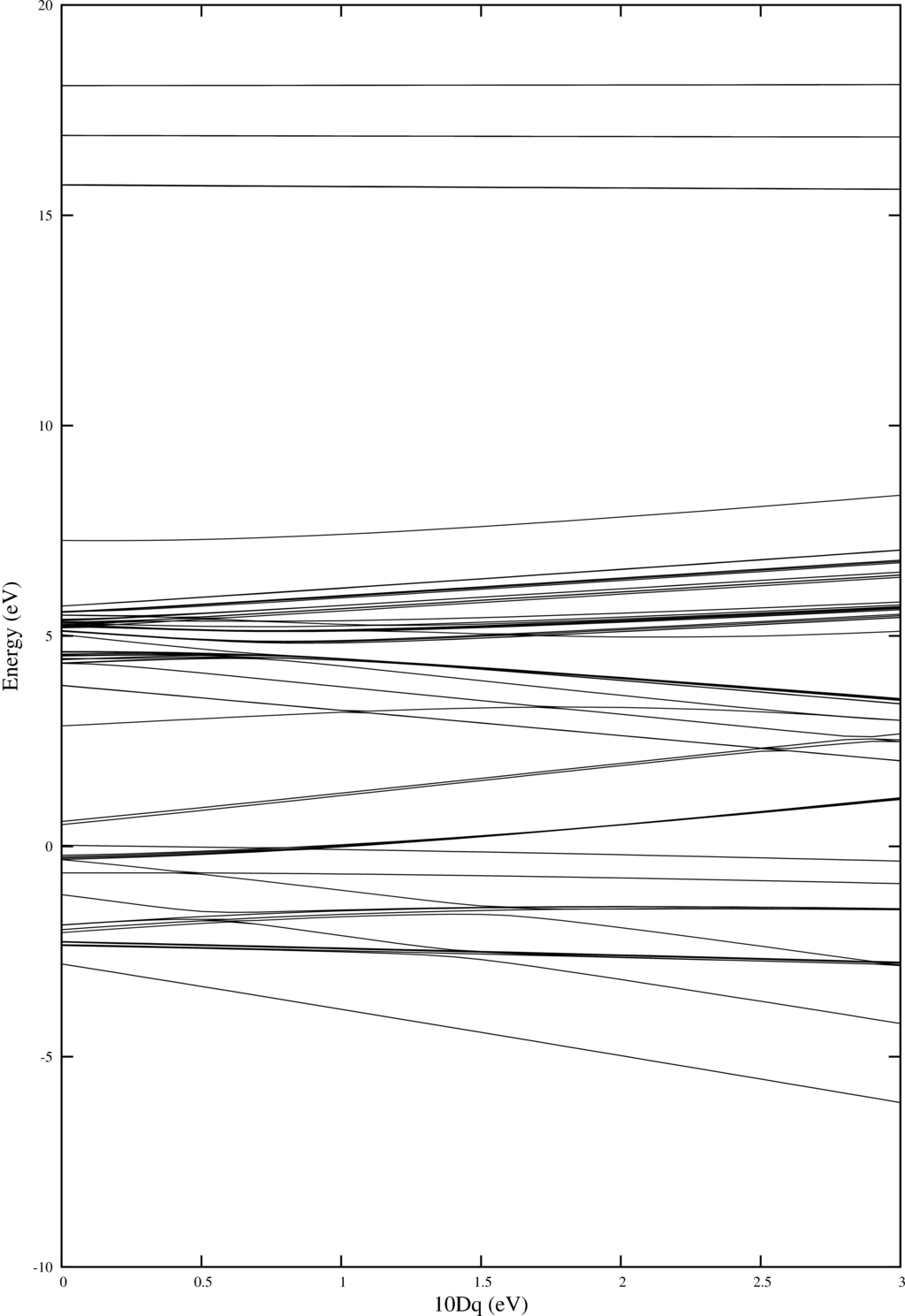 |
| Energy level diagram showing the energies of the different multiplets as a function of $10Dq$ |
|---|
The script does not write to standard output.