XAS $L_{2,3}$
Once the ground-state is calculated one can calculate the spectra. This example shows the Ni $2p$ to $3d$ excitations in NiO. Note that these excitations have an energy of more than 800 electron Volt, which is much higher than the chemically relevant energy scales. Non-the-less these kind of spectroscopy contain useful information on the local ground-state wave-function and the low energy effective Hamiltonian.
This tutorial compares calculated spectra to experiment. In order to make the plots you need to download the experimental data. You can download them in a zip file here nio_data.zip. Please unpack this file and make sure to have the folders NiO_Experiment and NiO_Radial in the same folder as you do the calculations. And as always, if used in a publication, please cite the original papers that published the data.
The input file to do these calculation is:
- XAS.Quanty
-- some example code -- This tutorial calculates the 2p to 3d x-ray absorption spectra of Ni in NiO using -- crystal field theory -- Within crystal-field theory the solid is approximated by a single atom in an effective -- potential. Although an extremely crude approximation it is useful for some cases. -- For correlated transition metal insulators it captures the right symmetry of the -- localized open d-shell. It is useful to determine magnetic g-factors, energies of d-d -- excitations or core level x-ray absorption. (2p to 3d excitations L23 edges) -- One should notice that the effective crystal-field potential is an affective potential -- it is there to mimic the interaction with neighboring ligand atoms. In real materials -- there do not exist such large electro static potentials. -- In order to do crystal-field theory for NiO we need to define a Ni d-shell. -- A d-shell has 10 elements and we label again the even spin-orbitals to be spin down -- and the odd spin-orbitals to be spin up. In order to calculate 2p to 3d excitations we -- also need a Ni 2p shell. We thus have a total of 10+6=16 fermions, 6 Ni-2p and 10 Ni-3d -- spin-orbitals NF=16 NB=0 IndexDn_2p={0,2,4} IndexUp_2p={1,3,5} IndexDn_3d={6,8,10,12,14} IndexUp_3d={7,9,11,13,15} -- just like in the previous example we define several operators acting on the Ni -3d shell OppSx =NewOperator("Sx" ,NF, IndexUp_3d, IndexDn_3d) OppSy =NewOperator("Sy" ,NF, IndexUp_3d, IndexDn_3d) OppSz =NewOperator("Sz" ,NF, IndexUp_3d, IndexDn_3d) OppSsqr =NewOperator("Ssqr" ,NF, IndexUp_3d, IndexDn_3d) OppSplus=NewOperator("Splus",NF, IndexUp_3d, IndexDn_3d) OppSmin =NewOperator("Smin" ,NF, IndexUp_3d, IndexDn_3d) OppLx =NewOperator("Lx" ,NF, IndexUp_3d, IndexDn_3d) OppLy =NewOperator("Ly" ,NF, IndexUp_3d, IndexDn_3d) OppLz =NewOperator("Lz" ,NF, IndexUp_3d, IndexDn_3d) OppLsqr =NewOperator("Lsqr" ,NF, IndexUp_3d, IndexDn_3d) OppLplus=NewOperator("Lplus",NF, IndexUp_3d, IndexDn_3d) OppLmin =NewOperator("Lmin" ,NF, IndexUp_3d, IndexDn_3d) OppJx =NewOperator("Jx" ,NF, IndexUp_3d, IndexDn_3d) OppJy =NewOperator("Jy" ,NF, IndexUp_3d, IndexDn_3d) OppJz =NewOperator("Jz" ,NF, IndexUp_3d, IndexDn_3d) OppJsqr =NewOperator("Jsqr" ,NF, IndexUp_3d, IndexDn_3d) OppJplus=NewOperator("Jplus",NF, IndexUp_3d, IndexDn_3d) OppJmin =NewOperator("Jmin" ,NF, IndexUp_3d, IndexDn_3d) Oppldots=NewOperator("ldots",NF, IndexUp_3d, IndexDn_3d) -- as in the previous example we define the Coulomb interaction OppF0 =NewOperator("U", NF, IndexUp_3d, IndexDn_3d, {1,0,0}) OppF2 =NewOperator("U", NF, IndexUp_3d, IndexDn_3d, {0,1,0}) OppF4 =NewOperator("U", NF, IndexUp_3d, IndexDn_3d, {0,0,1}) -- as in the previous example we define the crystal-field operator Akm = PotentialExpandedOnClm("Oh",2,{0.6,-0.4}) OpptenDq = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, Akm) -- and as in the previous example we define operators that count the number of eg and t2g -- electrons Akm = PotentialExpandedOnClm("Oh",2,{1,0}) OppNeg = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, Akm) Akm = PotentialExpandedOnClm("Oh",2,{0,1}) OppNt2g = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, Akm) -- new for core level spectroscopy are operators that define the interaction acting on the -- Ni-2p shell. There is actually only one of these interactions, which is the Ni-2p -- spin-orbit interaction Oppcldots= NewOperator("ldots", NF, IndexUp_2p, IndexDn_2p) -- we also need to define the Coulomb interaction between the Ni 2p- and Ni 3d-shell -- Again the interaction (e^2/(|r_i-r_j|)) is expanded on spherical harmonics. For the interaction -- between two shells we need to consider two cases. For the direct interaction a 2p electron -- scatters of a 3d electron into a 2p and 3d electron. The radial integrals involve -- the square of a 2p radial wave function at coordinate 1 and the square of a 3d radial -- wave function at coordinate 2. The transfer of angular momentum can either be 0 or 2. -- These processes are called direct and the resulting Slater integrals are F[0] and F[2]. -- The second proces involves a 2p electron scattering of a 3d electron into the 3d shell -- and at the same time the 3d electron scattering into a 2p shell. These exchange processes -- involve radial integrals over the product of a 2p and 3d radial wave function. The transfer -- of angular momentum in this case can be 1 or 3 and the Slater integrals are called G1 and G3. -- In Quanty you can enter these processes by labeling 4 indices for the orbitals, once -- the 2p shell with spin up, 2p shell with spin down, 3d shell with spin up and 3d shell with -- spin down. Followed by the direct Slater integrals (F0 and F2) and the exchange Slater -- integrals (G1 and G3) -- Here we define the operators separately and later sum them with appropriate prefactors OppUpdF0 = NewOperator("U", NF, IndexUp_2p, IndexDn_2p, IndexUp_3d, IndexDn_3d, {1,0}, {0,0}) OppUpdF2 = NewOperator("U", NF, IndexUp_2p, IndexDn_2p, IndexUp_3d, IndexDn_3d, {0,1}, {0,0}) OppUpdG1 = NewOperator("U", NF, IndexUp_2p, IndexDn_2p, IndexUp_3d, IndexDn_3d, {0,0}, {1,0}) OppUpdG3 = NewOperator("U", NF, IndexUp_2p, IndexDn_2p, IndexUp_3d, IndexDn_3d, {0,0}, {0,1}) -- next we define the dipole operator. The dipole operator is given as epsilon.r -- with epsilon the polarization vector of the light and r the unit position vector -- We can expand the position vector on (renormalized) spherical harmonics and use -- the crystal-field operator to create the dipole operator. -- x polarized light is defined as x = Cos[phi]Sin[theta] = sqrt(1/2) ( C_1^{(-1)} - C_1^{(1)}) Akm = {{1,-1,sqrt(1/2)},{1, 1,-sqrt(1/2)}} TXASx = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, IndexUp_2p, IndexDn_2p, Akm) -- y polarized light is defined as y = Sin[phi]Sin[theta] = sqrt(1/2) I ( C_1^{(-1)} + C_1^{(1)}) Akm = {{1,-1,sqrt(1/2)*I},{1, 1,sqrt(1/2)*I}} TXASy = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, IndexUp_2p, IndexDn_2p, Akm) -- z polarized light is defined as z = Cos[theta] = C_1^{(0)} Akm = {{1,0,1}} TXASz = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, IndexUp_2p, IndexDn_2p, Akm) -- besides linear polarized light one can define circular polarized light as the sum of -- x and y polarizations with complex prefactors TXASr = sqrt(1/2)*(TXASx - I * TXASy) TXASl =-sqrt(1/2)*(TXASx + I * TXASy) -- once all operators are defined we can set some parameter values. -- the value of U drops out of a crystal-field calculation as the total number of electrons -- is always the same U = 0.000 -- F2 and F4 are often referred to in the literature as J_{Hund}. They represent the energy -- differences between different multiplets. Numerical values can be found in the back of -- my PhD. thesis for example. http://arxiv.org/abs/cond-mat/0505214 F2dd = 11.142 F4dd = 6.874 -- F0 is not the same as U, although they are related. Unimportant in crystal-field theory -- the difference between U and F0 is so important that I do include it here. (U=0 so F0 is not) F0dd = U+(F2dd+F4dd)*2/63 -- in crystal field theory U drops out of the equation, also true for the interaction between the -- Ni 2p and Ni 3d electrons Upd = 0.000 -- The Slater integrals between the 2p and 3d shell, again the numerical values can be found -- in the back of my PhD. thesis. (http://arxiv.org/abs/cond-mat/0505214) F2pd = 6.667 G1pd = 4.922 G3pd = 2.796 -- F0 is not the same as U, although they are related. Unimportant in crystal-field theory -- the difference between U and F0 is so important that I do include it here. (U=0 so F0 is not) F0pd = Upd + G1pd*1/15 + G3pd*3/70 -- tenDq in NiO is 1.1 eV as can be seen in optics or using IXS to measure d-d excitations tenDq = 1.100 -- the Ni 3d spin-orbit is small but finite zeta_3d = 0.081 -- the Ni 2p spin-orbit is very large and should not be scaled as theory is quite accurate here zeta_2p = 11.498 -- we can add a small magnetic field, just to get nice expectation values. (units in eV... ) Bz = 0.000001 -- In mean field theory the neighboring Ni sites give an effective potential acting on the -- spin only when magnetically ordered. This exchange field in NiO is 6 J with J=27 meV. Hex = 6*0.027 -- see Europhys. Lett., 32 259 (1995) [ and Phys. Rev. B 82, 094403 (2010) ] -- the total Hamiltonian is the sum of the different operators multiplied with their prefactor Hamiltonian = F0dd*OppF0 + F2dd*OppF2 + F4dd*OppF4 + tenDq*OpptenDq + zeta_3d*Oppldots + Bz*(2*OppSz+OppLz) + Hex*sqrt(1/6)*(OppSx+OppSy+2*OppSz) -- We normally do not include core-valence interactions between filed and partially filled -- shells as it drops out anyhow. For the XAS we thus need to define a "different" -- (more complete) Hamiltonian. XASHamiltonian = Hamiltonian + zeta_2p * Oppcldots + F0pd * OppUpdF0 + F2pd * OppUpdF2 + G1pd * OppUpdG1 + G3pd * OppUpdG3 -- We saw in the previous example that NiO has a ground-state doublet with occupation -- t2g^6 eg^2 and S=1 (S^2=S(S+1)=2). The next state is 1.1 eV higher in energy and thus -- unimportant for the ground-state upto temperatures of 10 000 Kelvin. We thus restrict -- the calculation to the lowest 3 eigenstates. Npsi=3 -- in order to make sure we have a filling of 8 -- electrons we need to define some restrictions -- We need to restrict the occupation of the Ni-2p shell to 6 for the ground state and for -- the Ni 3d-shell to 8. StartRestrictions = {NF, NB, {"111111 0000000000",6,6}, {"000000 1111111111",8,8}} -- And calculate the lowest 3 eigenfunctions psiList = Eigensystem(Hamiltonian, StartRestrictions, Npsi) -- In order to get some information on these eigenstates it is good to plot expectation values -- We first define a list of all the operators we would like to calculate the expectation value of oppList={Hamiltonian, OppSsqr, OppLsqr, OppJsqr, OppSz, OppLz, Oppldots, OppF2, OppF4, OppNeg, OppNt2g}; -- next we loop over all operators and all states and print the expectation value print(" <E> <S^2> <L^2> <J^2> <S_z> <L_z> <l.s> <F[2]> <F[4]> <Neg> <Nt2g>"); for i = 1,#psiList do for j = 1,#oppList do expectationvalue = Chop(psiList[i]*oppList[j]*psiList[i]) io.write(string.format("%6.3f ",expectationvalue)) end io.write("\n") end -- calculating the spectra is simple and single line once all operators and wave-functions -- are defined. XASSpectra = CreateSpectra(XASHamiltonian, {TXASz,TXASr,TXASl}, psiList, {{"Emin",-10}, {"Emax",20}, {"NE",3000}, {"Gamma",0.1}}) -- XASSpectra will contain 9 spectra in the end. We have 3 functions in psiList and 3 -- polarizations. We furthermore define the energy range to be from -10 to +20 -- using 3000 energy points (delta E = 10 meV) and an internal lifetime during the calculation -- of 100 meV (Full width Half maximum) -- we can use several operations on a spectrum object. For one we can sum several spectra -- the function Spectra.Sum sums the spectra with the prefactors given in the list afterwards -- sum the spectra of the ground-state for different polarizations in order to get the -- isotropic spectrum XASIsoSpectra = Spectra.Sum(XASSpectra,{1,0,0, 1,0,0, 1,0,0}) -- broaden the spectra, note that a method changes the spectrum object, here we broaden by -- a Gaussian of FWHM 0.4 and Lorenzian of FWHM 1.0 XASSpectra.Broaden(0.4,1.0) -- we can also use energy dependent broadening by adding lists of the form {energy,FWHM} -- whereby the broadening used is linear interpolated between the energy points given XASIsoSpectra.Broaden(0.4, {{-3.7, 0.45}, {-2.2, 0.65}, { 0.0, 0.65}, { 8 , 0.80}, {13.2, 0.80}, {14.0, 1.075}, {16.0, 1.075}}) -- in order to plot the spectra we write them to file in ASCII format -- note that the calculated object, i.e. <psi | T^dag 1/(w-H+IG/2) T | psi> -- is complex. Minus the imaginary part is the absorption. XASSpectra.Print({{"file","XASSpec.dat"}}) XASIsoSpectra.Print({{"file","XASIsoSpec.dat"}}) -- in order to plot we use gnuplot. You can use any program, but gnuplot is nice as it can -- be called from within Quanty. We first define the gnuplot script as a string inside Quanty gnuplotInput = [[ set autoscale set xtic auto set ytic auto set style line 1 lt 1 lw 1 lc rgb "#000000" set style line 2 lt 1 lw 1 lc rgb "#FF0000" set style line 3 lt 1 lw 3 lc rgb "#000000" set xlabel "E (eV)" font "Times,12" set ylabel "Intensity (arb. units)" font "Times,12" set out 'XASSpec.ps' set size 1.0, 1.0 set terminal postscript portrait enhanced color "Times" 12 set multiplot layout 3, 3 plot "XASSpec.dat" u 1:(-$3 ) title 'z-polarized Sz=-1' with lines ls 1 plot "XASSpec.dat" u 1:(-$5 ) title 'z-polarized Sz= 0' with lines ls 1 plot "XASSpec.dat" u 1:(-$7 ) title 'z-polarized Sz= 1' with lines ls 1 plot "XASSpec.dat" u 1:(-$9 ) title 'r-polarized Sz=-1' with lines ls 1 plot "XASSpec.dat" u 1:(-$11) title 'r-polarized Sz= 0' with lines ls 1 plot "XASSpec.dat" u 1:(-$13) title 'r-polarized Sz= 1' with lines ls 1 plot "XASSpec.dat" u 1:(-$15) title 'l-polarized Sz=-1' with lines ls 1 plot "XASSpec.dat" u 1:(-$17) title 'l-polarized Sz= 0' with lines ls 1 plot "XASSpec.dat" u 1:(-$19) title 'l-polarized Sz= 1' with lines ls 1 unset multiplot energyshift=857.6 intensityscale=64 plot "XASSpec.dat" using ($1+energyshift):((-$3-$9-$15) * intensityscale) title 'isotropic theory' with lines ls 1,\ "NiO_Experiment/XAS_L23_PRB_57_11623_1998" using 1:2 title 'isotropic experiment' with lines ls 2 set size 1.0, 0.6 intensityscale=48 set out 'XASIsoSpec.ps' plot "NiO_Experiment/XAS_L23_PRB_57_11623_1998" using 1:2 title 'isotropic experiment' with filledcurves y1=0,\ "XASIsoSpec.dat" using ($1+energyshift):((-$3) * intensityscale) title 'isotropic theory' with lines ls 3 ]] -- next we save this string to a file file = io.open("XASSpec.gnuplot", "w") file:write(gnuplotInput) file:close() -- and finally call gnuplot to execute the script os.execute("gnuplot XASSpec.gnuplot") -- as I like pdf to view and eps to include in the manuel I transform the format os.execute(" ps2pdf XASSpec.ps ; ps2pdf XASIsoSpec.ps ; ps2eps XASIsoSpec.ps ; mv XASIsoSpec.eps temp.eps ; eps2eps temp.eps XASIsoSpec.eps ; rm temp.eps")
The resulting spectra are: (Experimental data from Alders et al. Phys. Rev. B 57, 11623 (1998).)
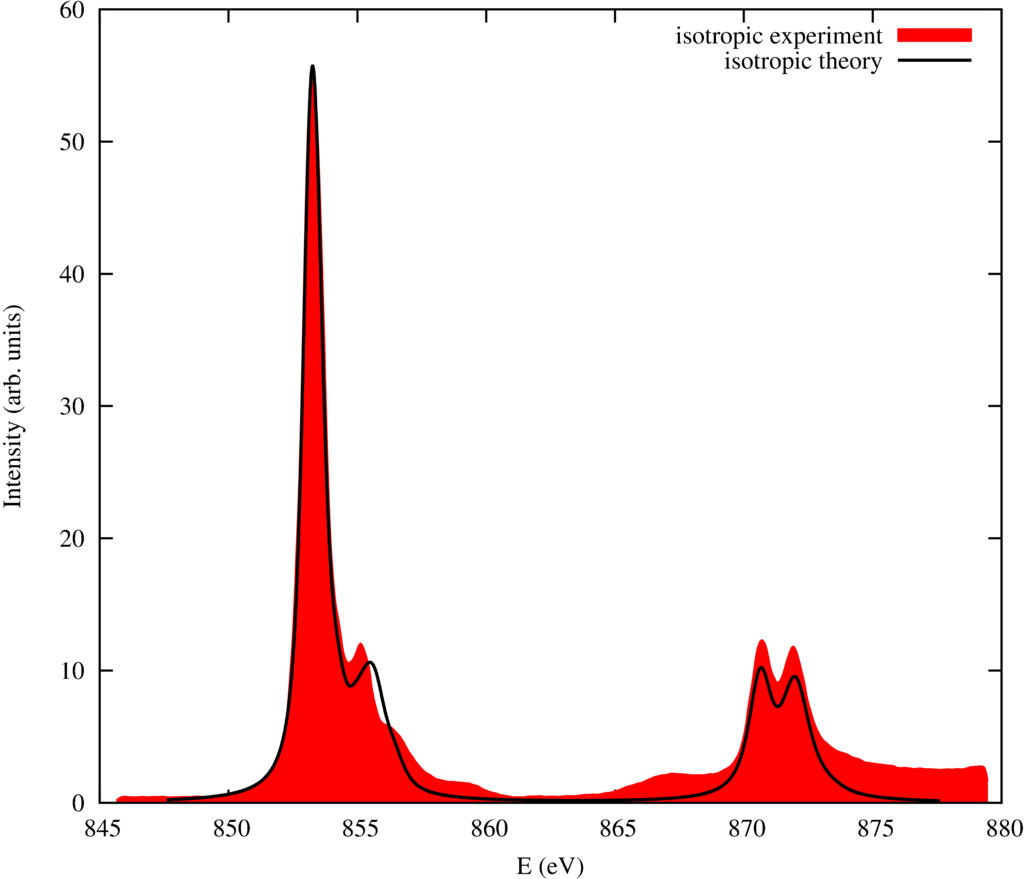
For NiO these spectra already are quite well reproduced on a crystal-field level. This reflects the strongly insulator and ionic behavior of NiO. There are still differences though in the energy range between 845 and 860 eV. In the next section we will calculate these spectra on a ligand field theory level and thereby improving the agrement between theory and experiment substantially.
The output of the script is:
- XAS.out
Start of BlockGroundState. Converge 3 states to an energy with relative variance smaller than 1.490116119384766E-06 Start of BlockOperatorPsiSerialRestricted Outer loop 1, Number of Determinants: 45 45 last variance 2.335271462951932E+00 Start of BlockOperatorPsiSerialRestricted Start of BlockGroundState. Converge 3 states to an energy with relative variance smaller than 1.490116119384766E-06 Start of BlockOperatorPsiSerial <E> <S^2> <L^2> <J^2> <S_z> <L_z> <l.s> <F[2]> <F[4]> <Neg> <Nt2g> -2.882 1.999 12.000 15.052 -0.813 -0.234 -0.306 -1.020 -0.878 2.009 5.991 -2.721 1.999 12.000 15.142 -0.002 -0.001 -0.330 -1.020 -0.878 2.011 5.989 -2.560 1.999 12.000 15.211 0.810 0.233 -0.349 -1.020 -0.878 2.012 5.988 Start of LanczosTriDiagonalizeMC Start of LanczosTriDiagonalizeMC Start of LanczosTriDiagonalizeMC Start of LanczosTriDiagonalizeMC Start of LanczosTriDiagonalizeMC Start of LanczosTriDiagonalizeMC Start of LanczosTriDiagonalizeMC Start of LanczosTriDiagonalizeMC Start of LanczosTriDiagonalizeMC Spectra printed to file: XASSpec.dat Spectra printed to file: XASIsoSpec.dat