FY $L_{2,3}M_{4,5}$
The absorption cross section is in principle measured using transmission. Transmission experiments in the soft-x-ray regime can be difficult as the absorption is quite high. Alternatively one can measure the reflectivity, which allows one to retrive the complete conductivity tensor using ellipsometry. As the x-ray wave-length is not large compared to the sample thickness this does not return the average sample absorption, but gives spatial information as well. Known as resonant scattering or reflectometry a beautiful technique, but might be overkill in some situations. A simple but effective way to measure the absorption cross section is to use the total electron yield, which can be measured by grounding the sample via an Ampare meter.
An alternative is to measure the fluorescence yield. Although not proportional to the absorption cross section \cite{Kurian:2012de,vanVeenendaal:1996tb,deGroot:1994tz} an extremely useful technique that contains similar information as absorption. Actually it is often more sensitive to differences in the ground-state and shows more detail in the spectral features. The calculation of fluorescence yield is similar to the calculation of absorption.
In the following example we calculate the excitation of a $2p$ electron into the $3d$ shell of Ni in NiO. ($L_{2,3}$ edge). We integrate over the decay of a $3d$ electron into the $2p$ orbital (removing an electron from the $3d$-shell i.e. $M_{4,5}$) We thus look at the $L_{2,3}$-$M_{4,5}$ FY spectra. (note that one should always list both the excitation as well as the decay channel as the spectra change between different channels).
The input is:
- FY_L23M45.Quanty
-- In this example we will calculate the fluorescence yield spectra -- One makes an excitation from 2p to 3d and then looks at a specific decay channel -- Or at the sum over all channels -- the spectra are integrated over the energy of the decay channel which allows for -- extreme efficient calculation of these spectra. -- Note that most detectors will not be equally sensitive to all possible photon energies -- and one thus would always measure some weighted sum over the different decay channels -- this file calculates the Ni L23M45 spectra. -- (L23, i.e. we excite from 2p to 3d) -- (M45, we decay from the 3d shell, into the 2p shell) -- we minimize the output by setting the verbosity to 0 Verbosity(0) -- In order to do crystal-field theory for NiO we need to define a Ni d-shell. -- A d-shell has 10 elements and we label again the even spin-orbitals to be spin down -- and the odd spin-orbitals to be spin up. In order to calculate 2p to 3d excitations we -- also need a Ni 2p shell. We thus have a total of 10+6=16 fermions, 6 Ni-2p and 10 Ni-3d -- spin-orbitals NF=16 NB=0 IndexDn_2p={0,2,4} IndexUp_2p={1,3,5} IndexDn_3d={6,8,10,12,14} IndexUp_3d={7,9,11,13,15} -- just like in the previous example we define several operators acting on the Ni -3d shell OppSx =NewOperator("Sx" ,NF, IndexUp_3d, IndexDn_3d) OppSy =NewOperator("Sy" ,NF, IndexUp_3d, IndexDn_3d) OppSz =NewOperator("Sz" ,NF, IndexUp_3d, IndexDn_3d) OppSsqr =NewOperator("Ssqr" ,NF, IndexUp_3d, IndexDn_3d) OppSplus=NewOperator("Splus",NF, IndexUp_3d, IndexDn_3d) OppSmin =NewOperator("Smin" ,NF, IndexUp_3d, IndexDn_3d) OppLx =NewOperator("Lx" ,NF, IndexUp_3d, IndexDn_3d) OppLy =NewOperator("Ly" ,NF, IndexUp_3d, IndexDn_3d) OppLz =NewOperator("Lz" ,NF, IndexUp_3d, IndexDn_3d) OppLsqr =NewOperator("Lsqr" ,NF, IndexUp_3d, IndexDn_3d) OppLplus=NewOperator("Lplus",NF, IndexUp_3d, IndexDn_3d) OppLmin =NewOperator("Lmin" ,NF, IndexUp_3d, IndexDn_3d) OppJx =NewOperator("Jx" ,NF, IndexUp_3d, IndexDn_3d) OppJy =NewOperator("Jy" ,NF, IndexUp_3d, IndexDn_3d) OppJz =NewOperator("Jz" ,NF, IndexUp_3d, IndexDn_3d) OppJsqr =NewOperator("Jsqr" ,NF, IndexUp_3d, IndexDn_3d) OppJplus=NewOperator("Jplus",NF, IndexUp_3d, IndexDn_3d) OppJmin =NewOperator("Jmin" ,NF, IndexUp_3d, IndexDn_3d) Oppldots=NewOperator("ldots",NF, IndexUp_3d, IndexDn_3d) -- as in the previous example we define the Coulomb interaction OppF0 =NewOperator("U", NF, IndexUp_3d, IndexDn_3d, {1,0,0}) OppF2 =NewOperator("U", NF, IndexUp_3d, IndexDn_3d, {0,1,0}) OppF4 =NewOperator("U", NF, IndexUp_3d, IndexDn_3d, {0,0,1}) -- as in the previous example we define the crystal-field operator Akm = PotentialExpandedOnClm("Oh",2,{0.6,-0.4}) OpptenDq = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, Akm) -- and as in the previous example we define operators that count the number of eg and t2g -- electrons Akm = PotentialExpandedOnClm("Oh",2,{1,0}) OppNeg = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, Akm) Akm = PotentialExpandedOnClm("Oh",2,{0,1}) OppNt2g = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, Akm) -- new for core level spectroscopy are operators that define the interaction acting on the -- Ni-2p shell. There is actually only one of these interactions, which is the Ni-2p -- spin-orbit interaction Oppcldots= NewOperator("ldots", NF, IndexUp_2p, IndexDn_2p) -- we also need to define the Coulomb interaction between the Ni 2p- and Ni 3d-shell -- Again the interaction (e^2/(|r_i-r_j|)) is expanded on spherical harmonics. For the interaction -- between two shells we need to consider two cases. For the direct interaction a 2p electron -- scatters of a 3d electron into a 2p and 3d electron. The radial integrals involve -- the square of a 2p radial wave function at coordinate 1 and the square of a 3d radial -- wave function at coordinate 2. The transfer of angular momentum can either be 0 or 2. -- These processes are called direct and the resulting Slater integrals are F[0] and F[2]. -- The second proces involves a 2p electron scattering of a 3d electron into the 3d shell -- and at the same time the 3d electron scattering into a 2p shell. These exchange processes -- involve radial integrals over the product of a 2p and 3d radial wave function. The transfer -- of angular momentum in this case can be 1 or 3 and the Slater integrals are called G1 and G3. -- In Quanty you can enter these processes by labeling 4 indices for the orbitals, once -- the 2p shell with spin up, 2p shell with spin down, 3d shell with spin up and 3d shell with -- spin down. Followed by the direct Slater integrals (F0 and F2) and the exchange Slater -- integrals (G1 and G3) -- Here we define the operators separately and later sum them with appropriate prefactors OppUpdF0 = NewOperator("U", NF, IndexUp_2p, IndexDn_2p, IndexUp_3d, IndexDn_3d, {1,0}, {0,0}) OppUpdF2 = NewOperator("U", NF, IndexUp_2p, IndexDn_2p, IndexUp_3d, IndexDn_3d, {0,1}, {0,0}) OppUpdG1 = NewOperator("U", NF, IndexUp_2p, IndexDn_2p, IndexUp_3d, IndexDn_3d, {0,0}, {1,0}) OppUpdG3 = NewOperator("U", NF, IndexUp_2p, IndexDn_2p, IndexUp_3d, IndexDn_3d, {0,0}, {0,1}) -- next we define the dipole operator. The dipole operator is given as epsilon.r -- with epsilon the polarization vector of the light and r the unit position vector -- We can expand the position vector on (renormalized) spherical harmonics and use -- the crystal-field operator to create the dipole operator. -- x polarized light is defined as x = Cos[phi]Sin[theta] = sqrt(1/2) ( C_1^{(-1)} - C_1^{(1)}) Akm = {{1,-1,sqrt(1/2)},{1, 1,-sqrt(1/2)}} TXASx = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, IndexUp_2p, IndexDn_2p, Akm) -- y polarized light is defined as y = Sin[phi]Sin[theta] = sqrt(1/2) I ( C_1^{(-1)} + C_1^{(1)}) Akm = {{1,-1,sqrt(1/2)*I},{1, 1,sqrt(1/2)*I}} TXASy = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, IndexUp_2p, IndexDn_2p, Akm) -- z polarized light is defined as z = Cos[theta] = C_1^{(0)} Akm = {{1,0,1}} TXASz = NewOperator("CF", NF, IndexUp_3d, IndexDn_3d, IndexUp_2p, IndexDn_2p, Akm) -- besides linear polarized light one can define circular polarized light as the sum of -- x and y polarizations with complex prefactors TXASr = sqrt(1/2)*(TXASx - I * TXASy) TXASl =-sqrt(1/2)*(TXASx + I * TXASy) -- we can remove zero's from the dipole operator by chopping it. TXASr.Chop() TXASl.Chop() -- the 3d to 2p dipole transition is the conjugate transpose of the 2p to 3d dipole transition TXASxdag = ConjugateTranspose(TXASx) TXASydag = ConjugateTranspose(TXASy) TXASzdag = ConjugateTranspose(TXASz) TXASldag = ConjugateTranspose(TXASl) TXASrdag = ConjugateTranspose(TXASr) -- once all operators are defined we can set some parameter values. -- the value of U drops out of a crystal-field calculation as the total number of electrons -- is always the same U = 0.000 -- F2 and F4 are often referred to in the literature as J_{Hund}. They represent the energy -- differences between different multiplets. Numerical values can be found in the back of -- my PhD. thesis for example. http://arxiv.org/abs/cond-mat/0505214 F2dd = 11.142 F4dd = 6.874 -- F0 is not the same as U, although they are related. Unimportant in crystal-field theory -- the difference between U and F0 is so important that I do include it here. (U=0 so F0 is not) F0dd = U+(F2dd+F4dd)*2/63 -- in crystal field theory U drops out of the equation, also true for the interaction between the -- Ni 2p and Ni 3d electrons Upd = 0.000 -- The Slater integrals between the 2p and 3d shell, again the numerical values can be found -- in the back of my PhD. thesis. (http://arxiv.org/abs/cond-mat/0505214) F2pd = 6.667 G1pd = 4.922 G3pd = 2.796 -- F0 is not the same as U, although they are related. Unimportant in crystal-field theory -- the difference between U and F0 is so important that I do include it here. (U=0 so F0 is not) F0pd = Upd + G1pd*1/15 + G3pd*3/70 -- tenDq in NiO is 1.1 eV as can be seen in optics or using IXS to measure d-d excitations tenDq = 1.100 -- the Ni 3d spin-orbit is small but finite zeta_3d = 0.081 -- the Ni 2p spin-orbit is very large and should not be scaled as theory is quite accurate here zeta_2p = 11.498 -- we can add a small magnetic field, just to get nice expectation values. (units in eV... ) Bz = 0.000001 -- the total Hamiltonian is the sum of the different operators multiplied with their prefactor Hamiltonian = F0dd*OppF0 + F2dd*OppF2 + F4dd*OppF4 + tenDq*OpptenDq + zeta_3d*Oppldots + Bz*(2*OppSz+OppLz) -- We normally do not include core-valence interactions between filed and partially filled -- shells as it drops out anyhow. For the XAS we thus need to define a "different" -- (more complete) Hamiltonian. XASHamiltonian = Hamiltonian + zeta_2p * Oppcldots + F0pd * OppUpdF0 + F2pd * OppUpdF2 + G1pd * OppUpdG1 + G3pd * OppUpdG3 -- We saw in the previous example that NiO has a ground-state doublet with occupation -- t2g^6 eg^2 and S=1 (S^2=S(S+1)=2). The next state is 1.1 eV higher in energy and thus -- unimportant for the ground-state upto temperatures of 10 000 Kelvin. We thus restrict -- the calculation to the lowest 3 eigenstates. Npsi=3 -- in order to make sure we have a filling of 8 -- electrons we need to define some restrictions -- We need to restrict the occupation of the Ni-2p shell to 6 for the ground state and for -- the Ni 3d-shell to 8. StartRestrictions = {NF, NB, {"111111 0000000000",6,6}, {"000000 1111111111",8,8}} -- And calculate the lowest 3 eigenfunctions psiList = Eigensystem(Hamiltonian, StartRestrictions, Npsi) -- In order to get some information on these eigenstates it is good to plot expectation values -- We first define a list of all the operators we would like to calculate the expectation value of oppList={Hamiltonian, OppSsqr, OppLsqr, OppJsqr, OppSz, OppLz, Oppldots, OppF2, OppF4, OppNeg, OppNt2g}; -- next we loop over all operators and all states and print the expectation value print(" <E> <S^2> <L^2> <J^2> <S_z> <L_z> <l.s> <F[2]> <F[4]> <Neg> <Nt2g>"); for i = 1,#psiList do for j = 1,#oppList do expectationvalue = Chop(psiList[i]*oppList[j]*psiList[i]) io.write(string.format("%6.3f ",expectationvalue)) end io.write("\n") end -- here we calculate the x-ray absorption spectra, not the main task of this file, but nice to do so we can compare XASSpectra = CreateSpectra(XASHamiltonian, {TXASz, TXASr, TXASl}, psiList, {{"Emin",-10}, {"Emax",20}, {"NE",3500}, {"Gamma",1.0}}); XASSpectra.Print({{"file","FYL23M45_XAS.dat"}}); -- and we calculate the FY spectra FYSpectra = CreateFluorescenceYield(XASHamiltonian, {TXASz, TXASr, TXASl}, {TXASxdag, TXASydag, TXASzdag}, psiList, {{"Emin",-10}, {"Emax",20}, {"NE",3500}, {"Gamma",1.0}}); FYSpectra.Print({{"file","FYL23M45_Spec.dat"}}); -- in order to plot both the XAS and FY spectra we can define a gnuplot script gnuplotInput = [[ set autoscale set xtic auto set ytic auto set style line 1 lt 1 lw 1 lc rgb "#000000" set style line 2 lt 1 lw 1 lc rgb "#FF0000" set style line 3 lt 1 lw 1 lc rgb "#00FF00" set style line 4 lt 1 lw 1 lc rgb "#0000FF" set xlabel "E (eV)" font "Times,10" set ylabel "Intensity (arb. units)" font "Times,10" set out 'FYL23M45.ps' set terminal postscript portrait enhanced color "Times" 8 size 7.5,6 set yrange [0:0.6] set multiplot layout 3, 3 plot "FYL23M45_XAS.dat" u 1:(-$3 ) title 'z-polarized Sz=-1' with filledcurves y1=0 ls 1 fs transparent solid 0.5,\ "FYL23M45_Spec.dat" u 1:(4*$2) title 'FY - x out' with lines ls 2,\ "FYL23M45_Spec.dat" u 1:(4*$4) title 'FY - y out' with lines ls 3,\ "FYL23M45_Spec.dat" u 1:(4*$6) title 'FY - z out' with lines ls 4 plot "FYL23M45_XAS.dat" u 1:(-$5 ) title 'z-polarized Sz= 0' with filledcurves y1=0 ls 1 fs transparent solid 0.5,\ "FYL23M45_Spec.dat" u 1:(4*$8) title 'FY - x out' with lines ls 2,\ "FYL23M45_Spec.dat" u 1:(4*$10) title 'FY - y out' with lines ls 3,\ "FYL23M45_Spec.dat" u 1:(4*$12) title 'FY - z out' with lines ls 4 plot "FYL23M45_XAS.dat" u 1:(-$7 ) title 'z-polarized Sz= 1' with filledcurves y1=0 ls 1 fs transparent solid 0.5,\ "FYL23M45_Spec.dat" u 1:(4*$14) title 'FY - x out' with lines ls 2,\ "FYL23M45_Spec.dat" u 1:(4*$16) title 'FY - y out' with lines ls 3,\ "FYL23M45_Spec.dat" u 1:(4*$18) title 'FY - z out' with lines ls 4 plot "FYL23M45_XAS.dat" u 1:(-$9 ) title 'r-polarized Sz=-1' with filledcurves y1=0 ls 1 fs transparent solid 0.5,\ "FYL23M45_Spec.dat" u 1:(4*$20) title 'FY - x out' with lines ls 2,\ "FYL23M45_Spec.dat" u 1:(4*$22) title 'FY - y out' with lines ls 3,\ "FYL23M45_Spec.dat" u 1:(4*$24) title 'FY - z out' with lines ls 4 plot "FYL23M45_XAS.dat" u 1:(-$11) title 'r-polarized Sz= 0' with filledcurves y1=0 ls 1 fs transparent solid 0.5,\ "FYL23M45_Spec.dat" u 1:(4*$26) title 'FY - x out' with lines ls 2,\ "FYL23M45_Spec.dat" u 1:(4*$28) title 'FY - y out' with lines ls 3,\ "FYL23M45_Spec.dat" u 1:(4*$30) title 'FY - z out' with lines ls 4 plot "FYL23M45_XAS.dat" u 1:(-$13) title 'r-polarized Sz= 1' with filledcurves y1=0 ls 1 fs transparent solid 0.5,\ "FYL23M45_Spec.dat" u 1:(4*$32) title 'FY - x out' with lines ls 2,\ "FYL23M45_Spec.dat" u 1:(4*$34) title 'FY - y out' with lines ls 3,\ "FYL23M45_Spec.dat" u 1:(4*$36) title 'FY - z out' with lines ls 4 plot "FYL23M45_XAS.dat" u 1:(-$15) title 'l-polarized Sz=-1' with filledcurves y1=0 ls 1 fs transparent solid 0.5,\ "FYL23M45_Spec.dat" u 1:(4*$38) title 'FY - x out' with lines ls 2,\ "FYL23M45_Spec.dat" u 1:(4*$40) title 'FY - y out' with lines ls 3,\ "FYL23M45_Spec.dat" u 1:(4*$42) title 'FY - z out' with lines ls 4 plot "FYL23M45_XAS.dat" u 1:(-$17) title 'l-polarized Sz= 0' with filledcurves y1=0 ls 1 fs transparent solid 0.5,\ "FYL23M45_Spec.dat" u 1:(4*$44) title 'FY - x out' with lines ls 2,\ "FYL23M45_Spec.dat" u 1:(4*$46) title 'FY - y out' with lines ls 3,\ "FYL23M45_Spec.dat" u 1:(4*$48) title 'FY - z out' with lines ls 4 plot "FYL23M45_XAS.dat" u 1:(-$19) title 'l-polarized Sz= 1' with filledcurves y1=0 ls 1 fs transparent solid 0.5,\ "FYL23M45_Spec.dat" u 1:(4*$50) title 'FY - x out' with lines ls 2,\ "FYL23M45_Spec.dat" u 1:(4*$52) title 'FY - y out' with lines ls 3,\ "FYL23M45_Spec.dat" u 1:(4*$54) title 'FY - z out' with lines ls 4 unset multiplot ]] -- write the gnuplot script to a file file = io.open("FYL23M45.gnuplot", "w") file:write(gnuplotInput) file:close() -- call gnuplot to execute the script os.execute("gnuplot FYL23M45.gnuplot") -- and transform the ps to pdf os.execute("ps2pdf FYL23M45.ps ; ps2eps FYL23M45.ps ; mv FYL23M45.eps temp.eps ; eps2eps temp.eps FYL23M45.eps ; rm temp.eps")
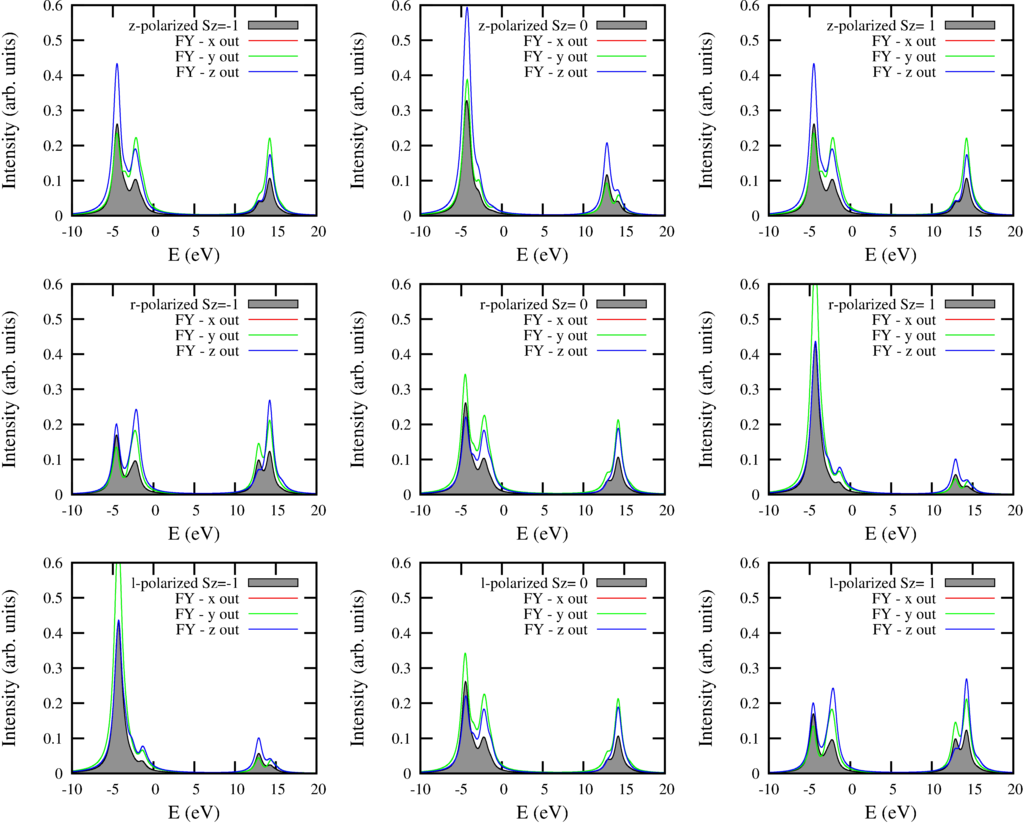
The script returns 9 plots with each 4 curves. The local ground-state of Ni in NiO is 3-fold degenerate in the paramagnetic phase ($S=1$) The different columns show the spectra for the states with different $S_z$. In the paramagnetic phase one should summ these 3 spectra, in a full magnetized sample one measurers either the left or the right column. The different rows the different incoming polarization. Top row z-polarized, middle right bottom left polarized light. The black filed curve shows the absorption cross section. The red, green and blue curve show the spectra for different outgoing polarization.
The script shows some information on the ground-state, here the text output.
- FY_L23M45.out
<E> <S^2> <L^2> <J^2> <S_z> <L_z> <l.s> <F[2]> <F[4]> <Neg> <Nt2g> -2.721 1.999 12.000 15.120 -0.994 -0.286 -0.324 -1.020 -0.878 2.011 5.989 -2.721 1.999 12.000 15.120 -0.000 -0.000 -0.324 -1.020 -0.878 2.011 5.989 -2.721 1.999 12.000 15.120 0.994 0.286 -0.324 -1.020 -0.878 2.011 5.989 Start of LanczosTriDiagonalizeKrylovRR Start of LanczosTriDiagonalizeKrylovRR Start of LanczosTriDiagonalizeKrylovRR Start of LanczosTriDiagonalizeKrylovRR Start of LanczosTriDiagonalizeKrylovRR Start of LanczosTriDiagonalizeKrylovRR Start of LanczosTriDiagonalizeKrylovRR Start of LanczosTriDiagonalizeKrylovRR Start of LanczosTriDiagonalizeKrylovRR