Hubbard model on a dimer
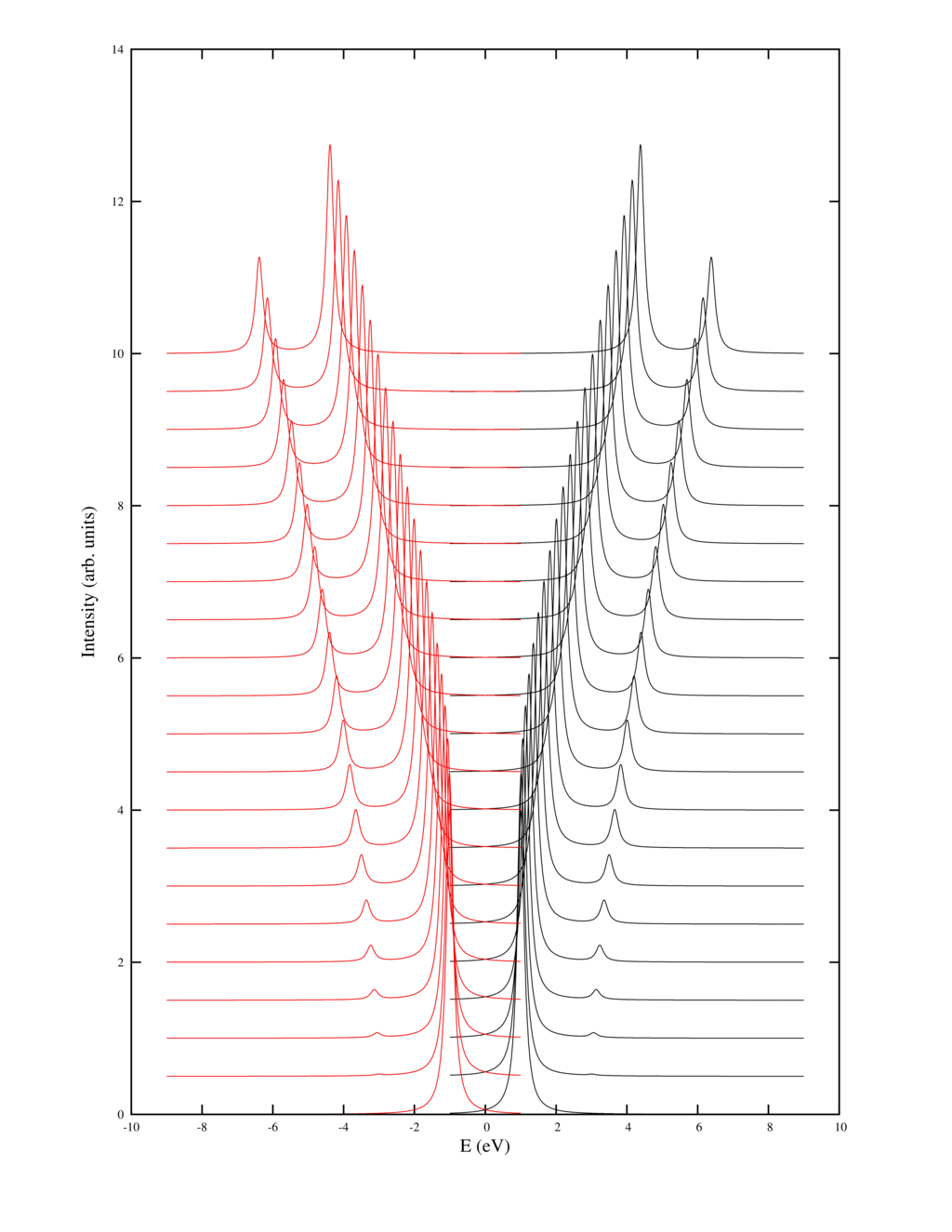
This example shows the effect of inter-site correlations in a two site Hubbard model, aka a H$_2$ molecule on the smallest basis possible. The solution of this problem is analytically known. The large $U$ limit is known as the Heither-London approximation.
The input code is:
- H2.Quanty
Verbosity(0) -- This example calculates the PES and IPES of a H2 molecule in the Hubbard model -- approximation -- we have two s-shells one centered around atom A, one around atom B -- in total there are thus 4 spin-orbitals NF=4 NB=0 IndexADn={0} IndexAUp={1} IndexBDn={2} IndexBUp={3} -- The Hamiltonian is given by a hopping from site A to B that conserves spin -- A Coulomb repulsion if the two electrons are on the same site -- A chemical potential that gives an onsite energy of -U/2 OppNAdn = NewOperator("Number", NF, 0, 0) OppNAup = NewOperator("Number", NF, 1, 1) OppNBdn = NewOperator("Number", NF, 2, 2) OppNBup = NewOperator("Number", NF, 3, 3) OppNA = OppNAup + OppNAdn OppNB = OppNBup + OppNBdn Oppt = NewOperator("Number", NF, {0,1,2,3}, {2,3,0,1}, {1,1,1,1}) OppU = OppNAup * OppNAdn + OppNBup * OppNBdn -- PES and IPES are electron annihilation and creation operators TPes = NewOperator("An", NF, 0) TIPes = NewOperator("Cr", NF, 0) -- the total number of states is 6. Npsi=6; StartRestrictions = {NF, NB, {"1111",2,2}}; psiList = Eigensystem(Oppt, StartRestrictions, Npsi); -- a loop creates U dependent spectra for i=0, 20 do U = 0.5*i Hamiltonian=Oppt + U * OppU - U/2 * (OppNA+OppNB) Eigensystem(Hamiltonian, psiList) PESIPES= CreateSpectra(Hamiltonian, {TPes, TIPes}, psiList[1], {{"Emin",-1}, {"Emax",9}, {"NE",1000}, {"Gamma",0.25}}) PESIPES.Print({{"file", string.format("PESIPES%i.dat",i)}}) end gnuplotInput = [[ set autoscale set xtic auto set ytic auto set style line 1 lt 1 lw 1 lc rgb "#000000" set style line 2 lt 1 lw 1 lc rgb "#FF0000" set xlabel "E (eV)" font "Times,12" set ylabel "Intensity (arb. units)" font "Times,12" set out 'H2.ps' set size 1.0, 1.0 set terminal postscript portrait enhanced color "Times" 8 plot for [i=0:20] 'PESIPES'.i.'.dat' using ( $1):(-(column(3))+i/2.) notitle with lines ls 1,\ for [i=0:20] 'PESIPES'.i.'.dat' using (-$1):(-(column(5))+i/2.) notitle with lines ls 2 ]] -- write the gnuplot script to a file file = io.open("H2.gnuplot", "w") file:write(gnuplotInput) file:close() -- call gnuplot to execute the script os.execute("gnuplot H2.gnuplot ; ps2pdf H2.ps")
The example produces a picture of the spectral function as output: